True or false finite mathematics

If you think the statement is true, then show that it is true. On the other hand, if you think the statement is false, then give an example that disproves the statement. For example, the statement “If A and B are matrices of the same order, then A – B = B – A” is false and an example that disproves it is 

For 

while 

Such an example is called a counterexample.

1. True or false: A system comprising two linear equations in two variables has a unique solution if and only if the straight lines represented by the equations are nonparallel.
2. True or false: Suppose the straight lines represented by a system of two linear equations in two variables are parallel to each other. Then the system has infinitely many solutions.
3. True or false: If A and B are matrices of the same order, then  .
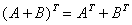4. True or false: If A and B are matrices such that AB and BA are both defined, then A and B must be square matrices.
5. True or false: If A is a square matrix with inverse 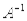 and c is a nonzero real number, then  .
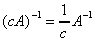6. True or false: If AX = B is a system of n linear equations in n unknowns and 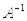does not exist, then AX = B does not have a unique solution.