Southern New Hampshire University Pre Calculus Two Discussion Questions

The height of the cylinder is 8 inches.

We’ll be analyzing the surface area of a round cylinder – in other words the amount of material needed to “make a can”.

A cylinder (round can) has a circular base and a circular top with vertical sides in between. Let r be the radius of the top of the can and let h be the height. The surface area of the cylinder, A, is A=2πr2+2πrh (it’s two circles for the top and bottom plus a rolled up rectangle for the side).

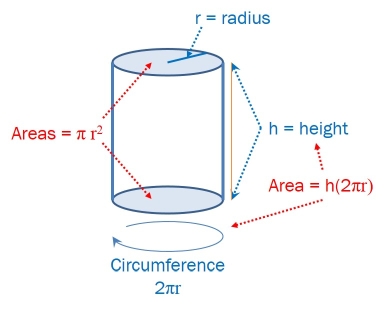
Part a: Assume that the height of your cylinder is 8 inches. Consider A as a function of r, so we can write that as A(r)=2πr2+16πr. What is the domain of A(r)? In other words, for which values of r is A(r) defined?

Part b: Continue to assume that the height of your cylinder is 8 inches. Write the radius r as a function of A. This is the inverse function to A(r), i.e to turn A as a function of r into. r as a function of A.

r(A)=

undefined

Hints:

• To calculate an inverse function, you need to solve for r. Here you would start with A=2πr2+16πr. This equation is the same as 2πr2+16πr−A=0 which is a quadratic equation in the variable r, and you can solve that using the quadratic formula.
• If you want to type in 3π+1 in Mobius, in text mode you can type in (3*pi+1)/(x+1). There is more information in the Introduction to Mobius unit.

Part c: If the surface area is 225 square inches, then what is the rardius r? In other words, evaluate r(225). Round your answer to 2 decimal places.

Hint: To compute a numeric square root such as 17.3−−−−√, you could

• Use a spreadsheet such as Microsoft Excel or OpenOffice Calc and type in =sqrt(17.3)
• Use a browser to connect to the Internet and type in sqrt(17.3) into a search field
• Use a calculator

The radius is inches if the surface area is 225 square inches.

I will need a step-by- explanation plus the answers. Let me know if you need anything else.