Precal 18 questions please help

1.

Solve the triangle.

A = 46°, a = 34, b = 27 (5 points)

B = 34.8°, C = 99.2°, c ≈ 28

B = 34.8°, C = 119.2°, c ≈ 37.3

Cannot be solved

B = 34.8°, C = 99.2°, c ≈ 46.7

2.

State whether the given measurements determine zero, one, or two triangles.

B = 84°, b = 28, c = 25 (5 points)

Two

One

Zero

3.

Two triangles can be formed with the given information. Use the Law of Sines to solve the triangles.

B = 46°, a = 12, b = 11 (5 points)

A = 38.3°, C = 95.7°, c = 8; A = 141.7°, C = 84.3°, c = 8

A = 51.7°, C = 82.3°, c = 8; A = 128.3°, C = 5.7°, c = 8

A = 38.3°, C = 95.7°, c = 15.2; A = 141.7°, C = 84.3°, c = 15.2

A = 51.7°, C = 82.3°, c = 15.2; A = 128.3°, C = 5.7°, c = 1.5

4.

The
given measurements may or may not determine a triangle. If not, then
state that no triangle is formed. If a triangle is formed, then use the
Law of Sines to solve the triangle, if it is possible, or state that the
Law of Sines cannot be used.

B = 111°, c = 8, b = 12 (5 points)

C = 38.5°, A = 30.5°, a ≈ 6.5

No triangle is formed.

C = 30.5°, A = 38.5°, a ≈ 6.5

The triangle cannot be solved with the Law of Sines.

5.

Solve the triangle.

A = 51°, b = 14, c = 6 (5 points)

No triangles possible

a ≈ 14.9, C ≈ 28.1, B ≈ 100.9

a ≈ 11.2, C ≈ 24.1, B ≈ 104.9

a ≈ 14.9, C ≈ 24.1, B ≈ 104.9

6.

Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary.

A = 50°, b = 31 ft, c = 18 ft (5 points)

427.45 ft²

179.34 ft²

213.73 ft²

558 ft²

7.

Determine
whether a triangle can be formed with the given side lengths. If so,
use Heron’s formula to find the area of the triangle. (5 points)

a = 240

b = 123

c = 207

9671.04

No triangle is formed.

9685.14

12,730.15

8.

A
building has a ramp to its front doors to accommodate the handicapped.
If the distance from the building to the end of the ramp is 19 feet and
the height from the ground to the front doors is 4 feet, how long is the
ramp? (Round to the nearest tenth.) (5 points)

5.7 ft

18.6 ft

4.8 ft

19.4 ft

10.

Let u = <-6, 3>, v = <1, 9>. Find u – v. (5 points)

<-15, 2>

<-9,-8>

<-5, 12>

<-7, -6>

11.

Let u = <-6, 1>, v = <-5, 2>. Find -4u + 2v. (5 points)

<34, -8>

<14, 0>

<14, 3>

<44, -12>

12.

Find a ⋅ b.

a = 9i – 6j, b = 5i + 5j (5 points)

-75

<45, -30>

<14, -1>

15

13.

Find the angle between the given vectors to the nearest tenth of a degree.

u = <8, 4>, v = <9, -9> (5 points)

81.6°

25.8°

35.8°

71.6°

14.

Determine whether the vectors u and v are parallel, orthogonal, or neither.

u = <1, -2>, v = <-4, 8> (5 points)

Orthogonal

Neither

Parallel

15.

Evaluate the expression.

r = <5, 9, -4>, v = <3, 3, -8>, w = <9, -6, -1>

v ⋅ w (5 points)

<-15, -27, -32>

0

17

<27, -18, 8>

16.

Express the complex number in trigonometric form.

-4i (5 points)

4(cos 180° + i sin 180°)

4(cos 270° + i sin 270°)

4(cos 90° + i sin 90°)

4(cos 0° + i sin 0°)

17.

Express the complex number in trigonometric form.

-6 + 6 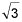i (5 points)

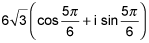
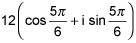
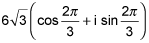
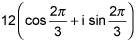
18.

Write the complex number in the form a + bi.

3(cos 60° + i sin 60°) (5 points)

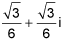
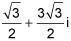
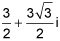
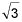+ i

19.

Two
forces with magnitudes of 90 and 50 pounds act on an object at angles
of 30° and 160°, respectively. Find the direction and magnitude of the
resultant force. Round to two decimal places in all intermediate steps
and in your final answer. (5 points