1.
The graph of f “(x) is continuous and decreasing with an x-intercept at x = 0. Which of the following statements is true? (4 points)
2.
The graph below shows the graph of f (x), its derivative f “(x), and its second derivative f “(x). Which of the following is the correct statement?
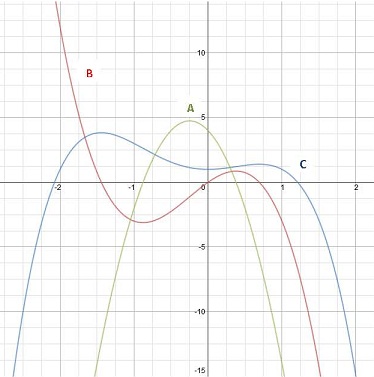(4 points)
3.
Below is the graph of f ‘(x), the derivative of f(x), and has x-intercepts at x = -3, x = 1 and x = 2. There are horizontal tangents at x = -1.5 and x = 1.5. Which of the following statements is true?
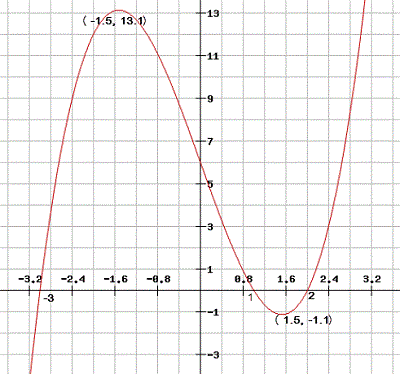(4 points)
4.
The graph of f ‘ (x), the derivative of f of x, is continuous for all x and consists of five line segments as shown below. Given f (-3) = 6, find the absolute maximum value of f (x) over the interval [-3, 0].
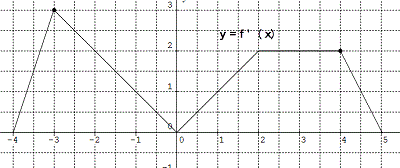(4 points)
5.
The graph of y = f ‘(x), the derivative of f(x), is shown below. Given f(2) = 8, evaluate f(-2).
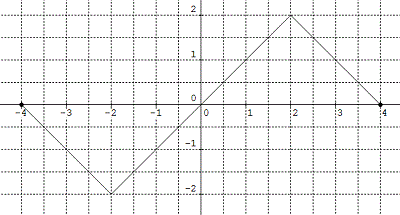(4 points)
1.
Which of the following functions grows the fastest as x goes to infinity? (4 points)
2.
Compare the rates of growth of f(x) = ecosx and g(x) = ex as x approaches infinity. (4 points)
3.
What does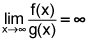 
show? (4 points)
4.
Which of the following functions grows at the same rate as 3x as x goes to infinity? (4 points)
5.
Which of the following functions grows the slowest as x goes to infinity? (4 points)
1.
The function f is continuous on the interval [3, 13] with selected values of x and f(x) given in the table below. Use the data in the table to approximate f ‘(12). (4 points)
| x | 3 | 4 | 7 | 11 | 13 |
|---|---|---|---|---|---|
| f(x) | 2 | 8 | 10 | 12 | 22 |
2.
f is a differentiable function on the interval [0, 1] and g(x) = f(4x). The table below gives values of f ‘(x). What is the value of g ‘(0.1)? (4 points)
| x | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
|---|---|---|---|---|---|
| f ‘(x) | 1 | 2 | 3 | -4 | 5 |
3.
f(x) and g(x) are a differentiable function for all reals and h(x) = g[f(2x)]. The table below gives selected values for f(x), g(x), f ‘(x), and g ‘(x). Find the value of h ‘(1). (4 points)
| x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f(x) | 0 | 3 | 2 | 1 | 2 | 0 |
| g(x) | 1 | 3 | 2 | 6 | 5 | 0 |
| f ‘(x) | 3 | 2 | 1 | 4 | 0 | 2 |
| g ‘(x) | 1 | 5 | 4 | 3 | 2 | 0 |
4.
The table of values below shows the rate of water consumption in gallons per hour at selected time intervals from t = 0 to t = 12.
Using a left Riemann sum with 5 subintervals, estimate the total amount of water consumed in that time interval. (4 points)
| x | 0 | 2 | 5 | 7 | 11 | 12 |
|---|---|---|---|---|---|---|
| f(x) | 5.7 | 5.0 | 2.0 | 1.2 | 0.6 | 0.4 |
5.
The function is continuous on the interval [10, 20] with some of its values given in the table above. Estimate the average value of the function with a Trapezoidal Sum Approximation, using the intervals between those given points. (4 points)
| x | 10 | 12 | 15 | 19 | 20 |
|---|---|---|---|---|---|
| f(x) | -2 | -5 | -9 | -12 | -16 |
1.
Let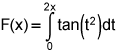 
. Use your calculator to find F”(1). (4 points)
2.
Pumping stations deliver oil at the rate modeled by the function D, given by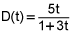 
with t measure in hours and and D(t) measured in gallons per hour. How much oil will the pumping stations deliver during the 4-hour period from t = 0 to t = 4? Give 3 decimal places. (4 points)
3.
A particle moves along the x-axis with velocity v(t) = t2 – 4, with t measured in seconds and v(t) measured in feet per second. Find the total distance travelled by the particle from t = 0 to t = 3 seconds. (4 points)
4.
Find the range of the function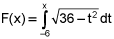 
. (4 points)
5.
Use the graph of f(t) = 2t – 5 on the interval [-2, 10] to write the function F(x), where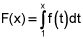 
. (4 points)
0 comments